Dudeneyn esittämä kysymys koski tasasivuisen kolmion muuntamista neliöksi leikkaamalla ja osien uudelleenjärjestämisellä. Tällaisia ongelmia, joita kutsutaan geometriseksi dissektioksi, kiinnostavat sekä pulmanratkaisijat että tutkijat. Alkuperäinen ratkaisu vaati neljä osaa, mutta kukaan ei ollut aiemmin todistanut, että parempaa ratkaisua olisi mahdotonta löytää.
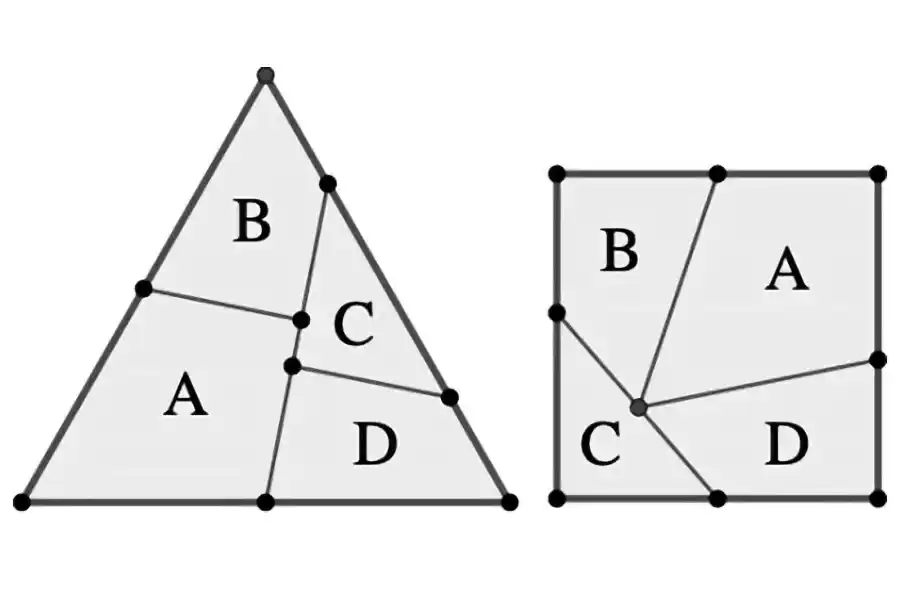
Kolmion jakamisen havainnollistaminen neliöksi Dudeneyn menetelmällä.
Luotto: Erik D. Demaine, Tonan Kamata, Ryuhei Uehara
Luotto: Erik D. Demaine, Tonan Kamata, Ryuhei Uehara
Kansainvälinen tiimi on äskettäin osoittanut, että neljä osaa on todellakin vähimmäismäärä. Heidän tutkimuksensa, jotka on julkaistu arXivissa, perustuvat innovatiiviseen menetelmään, joka käyttää vastaavuuskaavioita. Tämä lähestymistapa mahdollistaa leikattujen osien reunojen ja huippujen suhteiden analysoinnin.
Tutkijat hylkäsivät ensin mahdollisuuden ratkaisuun kahdella osalla ja tutkivat sitten systemaattisesti kaikki mahdolliset kolmen osan konfiguraatiot. Heidän johtopäätöksensä on kiistaton: mikään näistä konfiguraatioista ei johda täydelliseen neliöön. Tämä todistus merkitsee merkittävää edistystä dissektiokysymysten ymmärtämisessä.
Näiden tutkimusten sovellukset ylittävät puhtaiden matematiikan rajat. Ne löytävät kaikua sellaisilta aloilta kuin tekstiilien suunnittelu tai materiaalien valmistus. Tieteilijöiden kehittämä menetelmä voisi myös avata uusia mahdollisuuksia muiden vielä ratkaisemattomien dissektioproblemien ratkaisemiseen.
Tutkimus korostaa vastaavuuskaavioiden merkitystä dissektioiden analysoinnissa. Nämä graafiset työkalut mahdollistavat geometristen rajoitteiden visualisoimisen ja ratkaisun optimaalisuuden todistamisen. Ne tarjoavat näin uuden näkökulman ongelmiin, jotka ovat vaivanneet matemaatikkoja vuosisatojen ajan.
Tämä löytö ei vain päätä yhtä lukua matematiikan historiassa. Se luo perustan tuleville tutkimuksille, erityisesti leikkaus- ja kokoamisprosessien optimoinnissa. Tieteilijät suunnittelevat jo menetelmän soveltamista muihin geometrisiin muotoihin, mikä lupaa uusia edistysaskeleita tällä alalla.
Mitkä ovat geometriset dissektiot?
Geometrinen dissektio tarkoittaa muodon leikkaamista useiksi osiksi, joita voidaan järjestää uudelleen toisen muodon muodostamiseksi. Tämä käsite, joka juontaa juurensa antiikista, on sekä matemaattinen peli että työkalu käytännön ongelmien ratkaisemiseksi.
Yksinkertaisimmat dissektiot koskevat monikulmioita, kuten kolmioita ja neliöitä. Tavoitteena on usein minimoida tarvittavien osien määrä siirtymiseksi yhdestä muodosta toiseen. Tämä vaatii syvällistä ymmärrystä osallisten muotojen geometrisista ominaisuuksista.
Pulmien lisäksi geometrisilla dissektioilla on konkreettisia sovelluksia. Niitä käytetään esimerkiksi tekstiilikuosien suunnittelussa, materiaalien leikkaamisessa teollisuudessa ja jopa taiteessa. Niiden tutkiminen mahdollistaa resurssien käytön optimoinnin ja jätteen vähentämisen.
Ratkaisun optimaalisuuden todistaminen, kuten Dudeneyn tapauksessa, on ratkaiseva vaihe. Se varmistaa, että ollaan saavutettu mahdollinen tehokkain ratkaisu, mikä on tärkeää käytännön sovelluksille.
Kuinka vastaavuuskaaviot toimivat?
Vastaavuuskaaviot ovat graafisia työkaluja, joita käytetään geometristen dissektioiden analysoimiseen. Ne kuvaavat leikattujen osien reunojen ja huippujen välisiä suhteita graafien muodossa.
Tasasivuisen kolmion leikkaamisen tapauksessa neliöksi nämä kaaviot mahdollistavat osien liittämisen visualisoimisen. Ne auttavat tunnistamaan geometriset rajoitteet, jotka tekevät tietyistä konfiguraatioista mahdottomia.
Tämä menetelmä on erityisen hyödyllinen ratkaisun optimaalisuuden todistamisessa. Näyttämällä, että mikään vähemmän osia sisältävä konfiguraatio ei täytä rajoitteita, tutkijat voivat väittää, että ratkaisu on paras mahdollinen.
Vastaavuuskaaviot avaavat uusia näkökulmia monimutkaisempien dissektioproblemien ratkaisemiseen. Niiden soveltaminen voisi laajentua myös muille aloille, kuten insinöörirakenteiden suunnitteluun tai teollisten prosessien optimointiin.